
Introduzione
Che
cosa sono i frattali?
Come
si realizzano i frattali?
Area
Download
CARATTERISTICHE
Autosimilarità
Perimetro
infinito e area finita
Dimensione
non intera
Struttura
complessa a tutte le scale di riproduzione
Dinamica
caotica
PERSONAGGI
Niels
Fabian Helge von Koch
Waclaw
Sierpinski
Gaston
Maurice Julia
Benoit
Mandelbrot
TIPI DI FRATTALI
Curva
di von Kock
Triangolo
di Sierpinski
Tappeto
di Sierpinski
Insieme
di Mandelbrot
Insiemi
di Julia
Frattali
di Newton
Drago
frattale
Cattedrale
frattale
Icebergs frattali
Alberi frattali
Curva logistica
Nuvole frattali
FRATTALI E REALTA'
...fisiologia
umana
...arte
...musica
...altri
campi
Bibliografia
e indirizzi utili
METODO DI NEWTON
Questo metodo, detto anche metodo delle tangenti, permette di trovare le soluzioni approssimate di un'equazione , qualora si sappia che questa ammette uno zero in un dato intervallo. Seguiamo un esempio passo - passo.
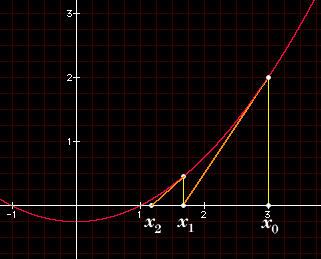
- Sappiamo che la soluzione dell'equazione f(x)=0, da un punto di vista grafico, è l'ascissa del punto di intersezione della curva y=f(x) con l'asse delle ascisse ( di equazione y=0).
- Immaginiamo di conoscere il grafico della curva.
- Diamo a x un valore che sembri vicino alla soluzione. Chiamiamo questo punto x0.
- Tracciamo una tangente alla curva nel punto di ascissa x0. L'ordinata del punto sarà f(x0).
- Troviamo l'ascissa del punto di intersezione della tangente con l'asse x. Chiamiamo questo punto x1.
- Il punto x1 è il nuovo valore approssimato della soluzione. .
- Ripetiamo il procedimento, tracciando la tangente alla curva nel suo punto di ascissa x1 .
- Otteniamo così una successione di numeri reali x0, x1, x2, x3..... che costituiscono approssimazioni via via migliori dello zero di f(x).
L'aspetto geometrico ora delineato può essere trasformato in un algoritmo eseguibile da un computer non appena si abbiano le seguenti abilità:
- Saper scrivere l'equazione di una retta per un punto: y-f(x0)=m(x-x0)
- Saper calcolare la derivata della curva in un punto di ascissa assegnata: poiché la nostra retta deve essere tangente alla curva nel punto x0, avremo m=f'(x0).
L'equazione della tangente alla curva y=f(x) nel suo punto di ascissa x0è perciò: y-f(x0)=f'(x0)(x-x0). - Saper trovare l'intersezione di una retta con l'asse delle x, ponendo nell'equazione y=0. Risulta x=x0-f(x0)/f'(x0). Chiamiamo questo punto x1.
xn+1=xn-f(xn)/f'(xn)
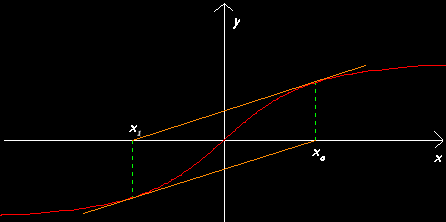 NOTA
NOTA
Se la curva cambia concavità nell'intervallo al quale appartiene lo zero della funzione, il metodo di Newton non sempre funziona, come si vede in questo esempio, in cui si entra in un ciclo infinito.